2장. 회귀 분석

실습

단순선형회귀분석

• Simple Linear Regression

회귀분석법

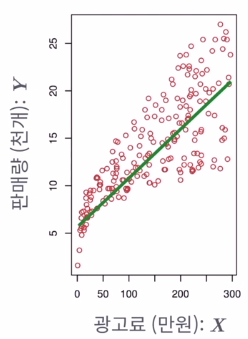
• 추세선

변수 표기

• N : 데이터의 개수
• X : input; 데이터; ex)’광고료’
• Y : Output; 해답; ex)’판매량’

문제 정의

• 데이터: N개의 FB광고 예산과 판매량
• 목표: 광고에 얼마를 투자했을 때 얼마나 팔릴까
• 광고 예산 => 학습된 모델 => 판매량
• 가정: 광고 예산과 판매량은 선형적 관계를 가진다
• Y = B0X + B1
  • 문제: 어떤 B0, B1이 좋은 것인가?

모델학습의 목표

• 완벽한 예측은 불가능
• 실제값과 모델이 예측하는 값을 최소한으로 하자
• Y ~ B0X + B1
  • 실제 값: y(i)
  • 예측 값: B0*x(i) +B1
  • 차이: y(i) - (B0*x(i) +B1)
  • 전체모델의 차이 Σ (y(i) - (B0*x(i) +B1))^2
• 차이를 최소로 하는 B0, B1을 구하자 (Loss function)
  • arg min(y(i) - (B0X(i) + B1))^2

산 정상 오르기

• 아무 곳에서나 시작했을 때, 가장 정상을 빠르게 찾아가는 방법
• 가정
  • 정상의 위치는 알 수 없다
  • 현재 나의 위치와 높이를 알 수 있다
  • 내 위치에서 일정 수준 이동할 수 있다
• 방법
  • 현재 위치에서 가장 경사가 높은 쪽을 찾는다
  • 오르막 방향으로 일정 수준 이동한다
  • 더 이상 높이의 변화가 없을 때까지 반복

산 내려가기

• Loss function을 최소로 만드는 B0, B1을 구하자

  다중선형회귀분석

• 각각 다른 입력 데이터의 기울기를 구한다

다항식 회귀 분석

• 단순한 선형회귀법은 데이터를 잘 설명하지 못한다
• n차식으로 표현 가능
• 판매량과 광고비의 관계를 2차식으로 표현해 보자
  • Y = B0X^2 + B1X + B2
  • X1 = X2
  • X2 = X
  • Y = B0X1 + B1X2 + B2
  • 다중회귀분석과 동일해진다