1장. 선형대수학.Numpy
Updated:
Scalar와 Vector
- 스칼라(Scalar)
- 길이, 넓이, 질량, 온도 크기만 존재하는 양
- 벡터(Vector)
- 속도, 위치 이동, 힘 크기와 방향이 모두 존재하는 양
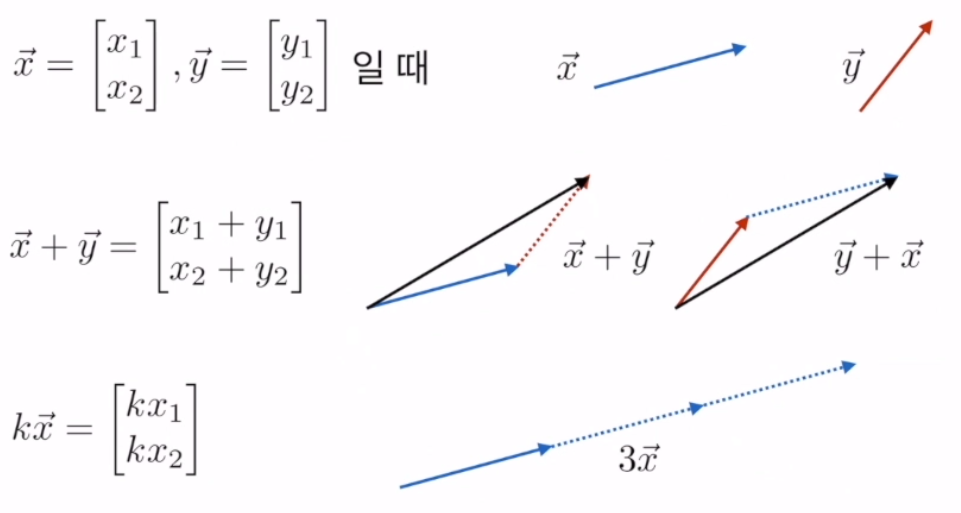
벡터
벡터 공간/내적
Norm
- 벡터의 크기
- n차원에서 원점과 n차원 점 사이의 거리
- 2차원에서 Norm이 1이라면 반지름이 1인 원
- 3차원에서 Norm이 1이라면 반지름이 1인 구
내적
- Euclidean inner project, Dot product
- 같은 차원끼리 곱한 후 더한다
- 차원이 다르면 수행할 수 없다
x = |x1| y = |y1| 일 떄 x*y = x1·y1 + x2*y2 + x3*y3
|x2| |y2|
|x3| |y3|
Matrix(행렬)
- 실수를 직사각형 모양으로 배열한 것
- 벡터를 쌓아 놓은것
- Matrix Arithmetic
- 같은 차원을 가진 행렬끼리만 더하거나 뺄 수 있다
- 행렬곱은 차원을 주의해야한다
Transpose(전치행렬)
- 원행렬의 행과 열을 뒤바꾼 행렬
Numpy
- Python에서 사용되는 과학 컴퓨팅용 라이브러리
- Python언어에서 기본으로 지원하지 않는 행렬과 같은 데이터 구조 지원 및 수학/과학 계산 함수 포함
- 머신러닝에서 대부분의 데이터를 행렬로 표현됨
간단한 형렬 연산
import numpy as np
A = np.array([[1, 2],
[3, 4]])
print(A)
#[[1 2]
# [3 4]]
print(A * 3)
#[[3 6]
# [9 12]]
print(A + A)
#[[2 4]
# [6 8]]
print(A - A)
#[[0 0]
# [0 0]]
print(A ** 2)
#[[ 1 4]
# [ 9 16]]
print(3 ** A)
#[[ 3 9]
# [27 81]]
print(A * A)
#[[ 1 4]
# [ 9 16]]
행렬곱셈
x = np.array([[1, 2], [3, 4]])
y = np.array([[3, 4], [3, 2]])
print(np.dot(x, y))
# [[9 8]
# [21 20]]
비교연산
a = np.array([[1, 2, 3, 4]])
b = np.array([[4, 2, 2, 4]])
print(a == b)
# [False, True, False, True]
print(a > b)
# [False, False, True, False]
논리 연산
a = np.array([[1, 1, 0, 0], dtype=bool])
b = np.array([[1, 0, 1, 0], dtype=bool])
print(np.logical_or(a,b))
# [True, True, True, False]
print(np.logical_and(a,b))
# [True, False, False, False]
a = np.array([1, 2, 3, 4, 5])
np.sum(a) # 15
a.sum() # 15
a.min() # 1
a.max() # 5
# index값을 가져온다
a.argmin() # 0
a.argmax() # 4
a = np.array([True, True, True)]
b = np.array([True, True, False)]
# all 모든값
np.all(a) # True
np.all(n) # False
# any 하나라도
np.any(a) # True
np.any(b) # True
Statistical
x = np.array([1, 2, 3, 1])
print(np.mean(x)) # 1.75
print(np.median(x)) # 1.5
print(np.std(x)) # 0.82915619758884995

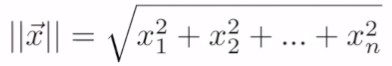
Leave a comment