4장. 추론 및 가설검정
Updated:
여러 가지 확률분포
- 이산 확률 분포
- 베르누이 분포
- 이항 분포
- 기하 분포
- 포아송 분포
- 연속확률 분포
- 균일 분포
- 정규 분포
베르누이 분포
- 베르누이 실행
- 각 시행은 성공과 실패 두 가지 중 하나의 결과를 가진
- 각 시행에서 성공할 확률은 p, 실패할 확률은 1-p
- 각 시행은 서로 독립으로 각시행의 결과가 다른 시행의 결과에 영향을 미치지 않음
- 확률 분포
| x | 0 | 1 |
|---|---|---|
| P(X=x | 1-p | p |
- 확률질량함수
f(x) = p , x = 1
1 - p , x = 0
이항 분포
- 베르누이 시행을 반복했을 때, 성공하는 횟수의 확률분포
- 이항 실험
- 성공확률이 동일한 베르누이 시행을 독립적으로 반복하는 실험
- 이항 확률변수
- 전체 시행 중 성공의 횟수에 따른 확률변수
- 이항 확률 변수 X의 확률 질량 함수
- 시행 횟수 n은 자연수이며, 성공확률 p는 0<=p<=1을 만족
X ~ B(n,p)
시행 횟수가 n, 성공확률이 p인 이항분포
stat_bin = scipy.stats.binom(n,p) #이항 분포 확률 변수
stat_bin.pmf(x축) # 확률 질량 함수 시각화
stat_bin.cdf(x축) # 누적 분포 함수 시각화
np.random.binamial(n, p, size) # 이항 분포 램덤 샘플
- n: 시행회수
- p: n=1이 나올 확률
- size = 표본 추출 작업 반복 횟수
초기하 분포
- 유한한 모집단에서 비복원 추출 시, 성공 횟수의 분포
- X : 표분 내에서 관심있는 범주(예: 불량품 개수)에 속하는 구성원소의 수
- 불량률 계산 등에서 많이 사용
X ~ Hyper(M,n,N)
- 모집단의 크기가 M이고, 표본의 크기가 n, 관심있는 범주(예: 불량품 개수)에 속하는 구성원소의 수가 N인 초기하분포
- 초기하 확률 변수 X의 확률 질량 함수
- 여기서 n은 D혹은 (N-D)보다 작거나 같은 수로 가정
- ex) 상자 안에 횐색 공 6개와 검은색 공 4개가 있을 때 5개의 공을 꺼낸 결과 흰공이 3개인 확률은?
10개 중 5개를 뽑는 경우의 수 가운데
흰색 공 6개 중 3개를 뽑고
검은색 공 5개 중 2개를 뽑을 확률
stat_hyp = scipy.stats.hypergeom(M, n, N) # 초기하 분포 확률 변수
stat_hyp.pmf(x축) # 확률 질량 함수 시각화
stat_hyp.cdf(x축) # 누적 분포 함수 시각화
np.random.hypergeometric(ngood, nbad, nsample, size) # 초기하 분포 램덤 샘플
- ngood(=n): 모집단 중 관심 있는 범주에 속하는 구성원소 수
- nbad(=M-n): 관심있는 표본 이외의 개수(ngood + nbad = M)
- nsample(=N): 표본의 크기
- size: 표본 추출 작업 반복 횟수
포아송 분포
- 연속된 시간 상에서 발생하는 사건은 매 순간 발생 가능
- 시행 횟수가 많고 순간의 성공확률은 작기 때문에 이항분포로 설명하기 어려움
- 단위시간/공간에 드물게 나타나는 사건의 횟수에 대한 확률 분포
-
연속적인 시간에서 매 순간에 발생할 것으로 기대되는 평균 발생 횟수를 이용해 주어진 시간에 실제로 발생하는 사건의 횟수 분포
- ex) 포아송 분포의 예시
일정 시간동안 발생하는 불량품의 수
일정 시간동안 톨게이트를 지나는 차량의 수
일정 페이지의 문장을 완성했을 때 발생하는 오타의 수
- X ~ Poi(𝜆)
- 평균적으로 𝜆 회 발생하는 사건의 발생 횟수에 대한 포아송분포
- 포아송 확률 변수 X의 확률 질량 함수
- 이항분포 B(n,p)에서 n이 매우 크고 p가 매우 작은 경우 𝜆=np인 포아송 분포로 근사 가능
균일 분포
- 구간 [a,b]에 속하는 값을 가질 수 있고 그 확률이 균일한 분포
- X ~ U(a,b)
- ex) 정육면체 주사위의 한 면이 나올 확률은 모두 1/6로 같다
- 균일 확률 변수 X의 확률 밀도 함수
a < b를 만족하는 임의의 두 실수 a, b에 대해 함수
f(x) = 1/b-a, a<=x<=b
0 , x<a or x>b
를 정의하면, f(x)를 확률 밀도 함수로 갖는
연속 확률 변수가 존재
stat_uni = scipy.stats.uniform(a,b) # 균일 분포 확률 변수
stat_uni.pmf(x축) # 확률 질량 함수 시각화
stat_uni.cdf(x축) # 누적 분포 함수 시각화
np.random.uniform(a,b,n) # 균일 분포 랜덤샘플
- a,b: 균일 분포의 구각
- n : 표본 추출 작업 반복 횟수
정규 분포
- 가장 많이 사용되는 유면한 분포
- 종형 곡선의 분포
- 평균 뮤(𝜇)와 표준편차 시그마(𝜎) 두 모수로 정의
- N(m,σ^2)로 표시
- 정규 분포를 나타내는 확률 밀도 함수
stat_nor= scipy.stats.norm(𝜇, 𝜎) #정규 분포 확률 변수
stat_nor.pmf(x축) # 확률 질량 함수 시각화
stat_nor.cdf(x축) # 누적 분포 함수 시각화
np.random.normal(𝜇, 𝜎, n) # 정규 분포 랜덤 샘플
- 𝜇: 평균
- 𝜎: 표준편차
- n :표본추출작업반복횟수
표준 정규 분포
- 정규 분포의 표준 분포
- 평균 뮤(𝜇)=1, 표준 편차 시그마(𝜎)=1로 둔 정규 분포Z
- 표준 정규 분포의 확률 밀도 함수
통계적 추론
- 표본이 갖고 있는 정보를 분석하여 모수를 추론
- 모수에 대한 가설의 옳고 그름을 판단
- 표본으로 전체 모집단의 성질을 추론하므로 오류 존재(이 부정확도를 반드시 언급해야 함)
- 조사자의 관심에 따라 모수 추정 혹은 가설검정으로 구분
모수 추정
- 모수에 대한 추론 혹은 추론치 제시
- 수치화 된 정확도 제시
모평균 점추정
- 점추정
- 추출된 표본으로부터의 모수의 값에 가까울 것이 예상되는 하나의 값을 제시
- 모집단의 모수인 평균 𝜇의추정
- 모집단에서 크기가 n 인 표본을 n개의 확률변수 𝑋1,𝑋2,…,𝑋𝑛로 표현 했을때, 모평균의 추정량 중, 직관적으로 타당한 것은 표본 평균
모평균 구간 추정
- 구간추정
- 하나의 값 대신 모수를 포함할 것이 예상되는 적절한 구간을 제시
- 신뢰 구간
- 추정량의 분포를 이용하여 표본으로부터 모수의 값을 포함하리라 예상되는 구간
- (작은값(하한), 큰값(상한))의 형태
- 신뢰 수준
- 신뢰구간이 모수를 포함할 확률을 1보다 작은 일정한 수준에서 유지할때 확률이 신뢰수준
- 신뢰수준은 90%, 95%, 99%등으로 정함
- 모평균 𝜇의신뢰구간
- 𝜇의분포: 모집단의정규분포, 표준편차(𝜎) 가주어짐
- 추정량ത𝑋의분포: 평균이𝜇, 표준편차가𝜎/𝑛^1/2인분포N(0,1)
- Z𝑎/2는N(0,1) 의상위𝑎/2의확률을주는값
- 모평균𝜇에대한신뢰구간
- 예) N(100, 10) 인 분포로부터 크기가 15인 표본을 추출해 표본평균 𝑥 = 105 일 때, 모평균에 대한 95% 신뢰구간:
통계적 가설 검정
가설검정
- 모집단의 특성이나 모수에 대한 주장이 있을때,이 주장의 옳고 그름을 표본자료를 이용하여 판단하는 방법
- 가설
- 모수에 대한 주장
- 통계적 가설 검정(검정)
- 주어진 가설을 표본 자료로부터 얻은 정보를 통해 검토하는 과정
귀무가설과대립가설
- 귀무가설
- 기본적인 가설
- 대립가설
- 자료를 통하여 입증하고자 하는 가설
- 비교하고 싶은 가설
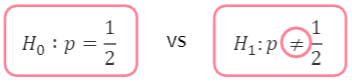
- ex) 하나의 동전을 던지면 앞면이 나올 확률을 1/2이라 가정할 때, 진짜 앞면이 ½의 확률로 나올지에 대한 검정
- 양측가설
- 단측가설
통계적 가설 검정
- 설정한 가설에 대한 옳고 그름을 표본자료를 통하여 검정, 두 가설 중 옳다고 판단할 수 있는 하나의 가설을 선택
- 표본 자료가 대립 가설을 지지하면 대립 가설 채택
- 표본 자료가 대입 가설을 지지하지 못하면 귀무 가설 채택
- 대입 가설을 채택하는 경우
- 귀무 가설 기각
- 귀무가설을 채택하는 경우
- 귀무 가설을 채택 or 귀무 가설을 기각할 수 없다
귀무 가설을 기준으로 한 표현 사용
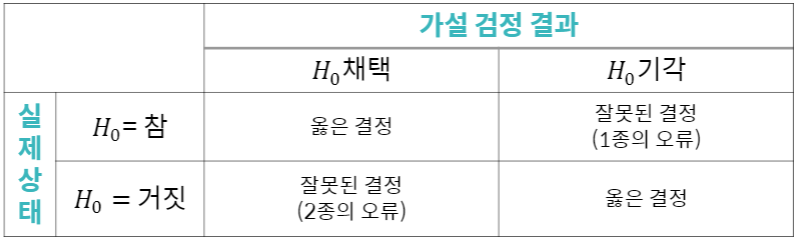
오류의 종류
- 1종 오류 : 귀무 가설이 참일 때 귀무 가설을 기각하는 경우
- 2종 오류 : 귀무 가설이 거짓일 때 귀무 가설을 채택하는 경우
- 가설 검정은 표본 자료만으로 모집단에 대한 가설을 검토하므로 오류 존재
- 바람직한 가설 검정은 두 오류를 최소화하는 것
- 두 오류를 동시에 최소화하는 검정은 존재하지 않거나 찾기 어려움
- 1종 오류를 범할 확률과 2종 오류를 범할 확률은 반비례 관계
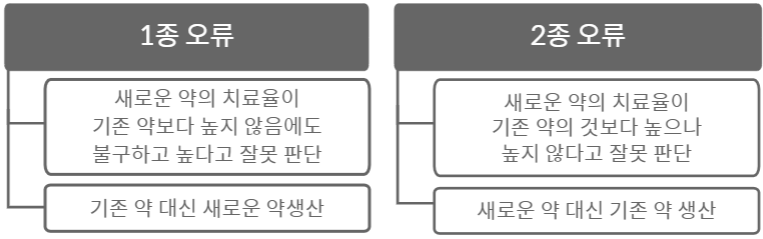
- 1종오류를 범할 때 더 큰손실이나 비용이 발생하는 경우가 많음
예) 𝐻0: 새로운 약의 치료율이 기존 약보다 높지 않다.
𝐻1: 새로운 약의 치료율이 기존 약보다 높다.
- 전통적인 통계학에서의 검정
- 1종 오류를 점할 확률을 우성 최소화
- 이후 2종 오류를 범할 확률을 최소화
유의수준
- Significance level, 𝛼
- 1종 오류를 범할 확률에 대한 최대 허용 한계 고정값
- 일반적으로 유의수준 𝛼의 값으로 0.01~ 0.10 사이의 작은값을 사용
검정의 종류와 과정
- 가설 설정
- 표본 자료의 관측
- 가설 검정에 사용할 통계량 선택(검정 통계량)
- 관측값 계산
- 기각역/ 유의 확률 계산
- 검정 결롸 해석 및 가설 채택
검정 통계량
- 가설 검정에 사용되는 통계량
- 가설 검정의 결과를 결정하는데 이용되는 표본의 함수
- 𝑋를 관측하여 그 값으로부터 𝜇에 대한 가설검정을 결정할 때 검정통계량으로 사용
검정을 위한 기준
기각역
- 𝑋가 취하는 구간중에서 𝐻0을 기각하는 구간
- R ∶ 𝑋≤𝑐로표현
- 𝑋가 c이하면 𝐻0을 기각한다고 판단
- 기각역의 올바른 선택이 검정의 가장 중요한 부분
- 바람직한 각역은 두 오류를 범할 확률을 최소화하는 것
유의 확률(P_value)
- 표본자료가 대립가설을 지지하는 정도를 0과 1사이의 숫자로 나타낸 최소의 유의 수준 값
- P-value 라고 부르기도 함
- 표준 정규 분포표를 이용해 P값을 구해야 함
- 유의 수준과 P값을 비교
- 유의수준 > P값인 경우: H를 기각
- 유의수준 < P값인 경우: H를 기각할 수 없음
가설검정종류
이항 검정
- 이항분포를 이용하여 베르누이 확률 변수의 모수 𝑝에 대한 가설 조사
- 베르누이 값을 가지는 확률변수의 분포를 판단
예) 어떤 동전을 던질때, 앞면이 나올 확률 𝑝=0.5인
공정한 동전인지 알아보는 검정 귀무 가설: 𝑝=0.5 vs 대립가설: 𝑝≠0.5
scipy.stats.binom_test(x, n, p, alternative='')
# 이항 검정의 유의 확률을 구해주는 함수
- x= 검정통계량, 1이 나온 횟수
- n = 총시도횟수
- p = 모수 p 값
- 양측검정: alternative = ‘two-sided’
- 단측검정:alternative = ‘one-sided’
모평균 가설 검정
- 표본의 크기가 클 때, 모평균𝜇이 정규분포를 따른다는 가정하에 중심 극한 정리에 의해 정규분포에 근사함
- 가설 검정을 하기 위한 검정 통계량𝑋를 표준화시키면
- 단측 검정
- 양측 검정
def ztest(stat, mu, sigma):
z = (stat.mean() - mu) / (sigma*sqrt(len(stat)))
return (2 * (1-sp.stats.norm.cdf(z)))
# 모평균 가설 검정 함수. 유의 확률 출력
- stat: 검정 통계량
- mu: 모평균
- sigma: 모표준 편차

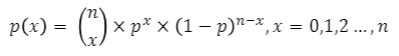
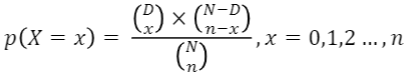
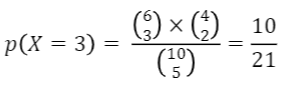
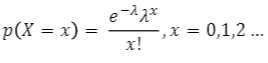
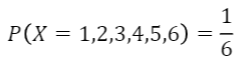
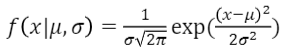
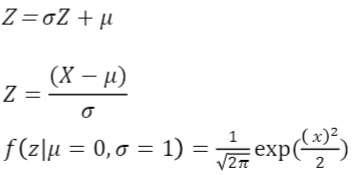
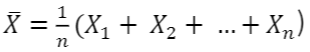
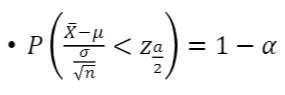
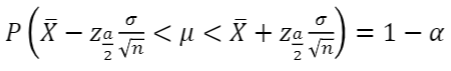
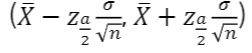
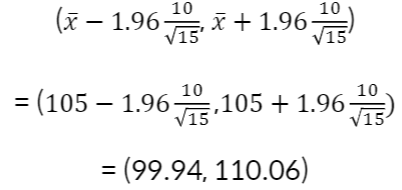

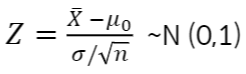


Leave a comment