2장. 논리적인 자료의 요약
Updated:
중심위치의 측도
수치를 통한 연속형 자료 요약
- 그림이나 도표에 의한 분석의 단점
- 작성자의 주관적 판단에 따라 달라지므로 일관성 및 객관성이 부족
- 시각적 자료로는 이론적 근거 제시가 쉽지 않음
- 많은 양의 자료를 의미 있는 수치로 요약하여 대략적인 분포상태를 파악 가능하므로 단점 보완 가능
- 중심위치의 측도(measure of center)
- 자료의 중심위치를 나타냄
2. 퍼진 정도의 측도(measure of dispersion) - 자료가 각 중심위치로부터 얼마나 흩어져 있는지 나타냄 3. 도수분포표에서의 자료의 요약
- 자료가 이미 그룹화된 경우의 수치 요약 방법 4. 상자 그림
- 사분위수, 최소값, 최대값 등을 이용한 요약 방법
중심위치의 측도
- 중심 위치값 결정 -> 중심위치의 측도 -> 평균, 중앙값, 최빈값
평균(Mean)
np.mean()
- 중심위치의 측도 중에서 가장 많이 사용되는 방법
- 모든 관특값의 합을 자료의 개수로 나눈 것
-
관측값들의 무게중심
- 평균의 특징
- 관측값의 산술평균으로 사용
- 통계에서 기초적인 통계 수치로 가장 많이 사용
- 극단적으로 큰 값이나 작은 값의 영향을 많이 받음
중앙값
np.median()
- 전체 관측값을 정렬했을 때 가눙데에 위치하는 값
- 자료의 개수(n)가 홀수인 경우
(n+1)/2번째 관측값 - 자료의 개수(n)가 짝수인 경우
n/2번째 관측값과 n/2+1번째 관측값의 평균 - 중앙값의 특징
- 관측값을 크기 순서대로 배열할 때 중앙에 위치
- 가운데에 위치한 값 이외의 값의 크기는 중요하지 않음
- 관측삾의 변화에 민감하지 않고, 극단값의 영향을 받지 않음
최빈값(Mode)
stats.mode()
- 관측값 중 가장 자주 나오는 값
-
이산형/범주형 자료에서 많이 사용
- 최빈값의 특징
- 연속형 자료에서 같은 값이 나오는 경우는 흔치 않으므로 최빈값을 사용하기 부적절
- 단봉형 분포를 갖는 자료에서만 유용
평균, 중앙값, 최빈값의 비교
- 사용빈도
- 평균 > 중앙값 > 최빈값
- 평균
- 이해하기 쉽고 통계적으로 가장 많이 사용
- 관측값이 골고루 반영
- 극단값으로 인한 영향을 많이 받음
- 중앙값
- 중앙 부분 외 관측값의 변화에 민감하지 않음
- 극단값으로 인한 영향을 받지 않음
- 극단값이 있는 경우
- 극단값의 영향을 배제하고 싶으면 중앙값 사용
- 전체 관측값을 모두 포함하고 싶으면 평균 사용
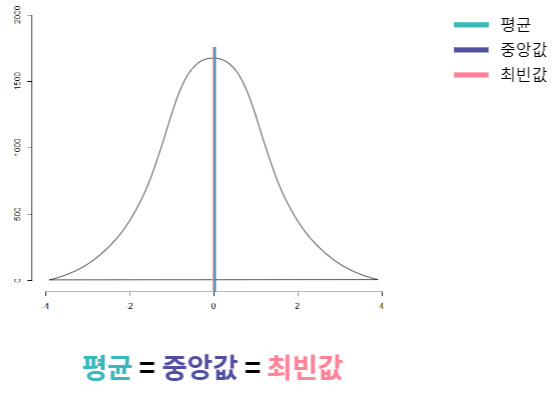
- 평균, 중앙값, 최빈값의 비교: 단봉형 대칭
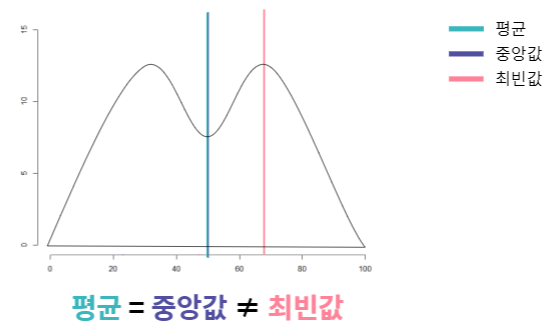
- 평균, 중앙값, 최빈값의 비교: 이봉형 대칭
-
다봉형 분포에서 최빈값은 중심위치의 측도로 부적합
-
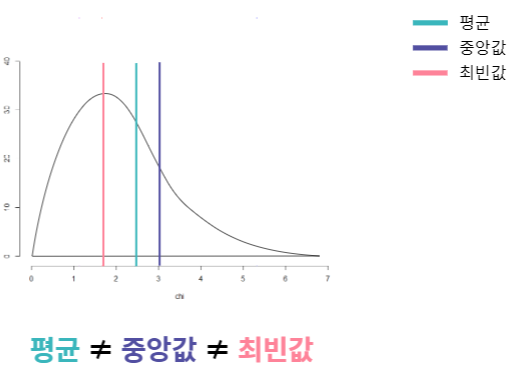
평균, 중앙값, 최빈값의비교:비대칭분포
- 왼쪽으로 치우친 분포
- 평균 > 중앙값
- 오른쪽으로 치우친 분호
- 평균 < 중앙값
퍼진 정도의 측도
- 중심위치만으로 분포를 파악하기에 부족
- 중심위치 측도 외에 분포가 퍼진 정도를 측도할 수치가 필요
- 분산, 표준편차, 범위, 사분위수 등을 퍼진 정도의 측도로 사용
분산
variance()
- 자료가 얼마나 흩어졌는지 숫자로 표현
- 각 관측값이 자료의 평균으로부터 떨어진 정도
- 작을수록 퍼진 정도가 작고 클수록 퍼진 정도가 크다
- 관측값에 대한 편차 = (관측값-평균)
- 편차의 합은 항상 0
- 음의 편차를 제곱하여 양수로 바꿀수 있다
- 편차 제곱합의 평균
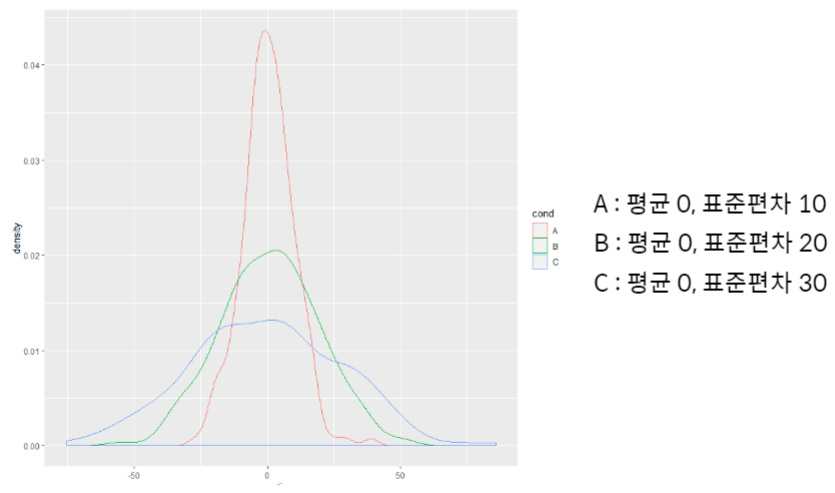
표준편차
stdev()
- 분산의 단위 = 관측값의 단위의 제곱
- 관측값의 단위와 불일치
- 분산의 양의 제곱근은 관측값과 단위가 일치
- 분산의 양의 제곱근을 표준평차라 라고 s로 표기
범위(Range)
np.max()-np.min()
- 관측값에서 가장 큰 값과 가장 작은 값의 차이
- 장점
- 간편하게 구할 수 있고 해석이 용이함
- 단점
- 중간에 위치한 값은 고려되지 않음
- 극단값의 영향이 클 수 있음
백분위수
np.percentile()
- 중앙값을 확장한 개념
- 자료를 순서대로 정렬했을 때 백분율로 특정 위치의 값을 표현
- 제 100xp 백분위수를 구하는 방법
1. 관측값을 오름차순으로 배열
2. 관측값의 개수(n)에 p를 곱셈
3-1. n*p가 정수인 경우
n*p번째로 작은 관측값과
n*p+1번째로 작은 관측값의 평균
3-2. n*p가 정수가 아닌 경우
n*p에서 정수 부분에 1을 더한 값 m을 구한 후
m번째로 작은 관측값
사분위수
np.percentile(25)
np.percentile(50)
np.percentile(75)
- 백분위수의 일종으로 전테를 사등분하는 값
- 제1, 2, 3 분위수를 각각 Q1, Q2, Q3으로 표시
제 1 사분위수 : Q1 = 제 25백분위수
제 2 사분위수 : Q1 = 제 50백분위수
제 3 사분위수 : Q1 = 제 75백분위수
- 중앙값은 전체의 1/2에 위치하는 값이므로 제 2사분위수 및 제 50백분위수
사분위수 범위
- 제 3사분위수롸 1사분위수 사이의 거리
- 사분위수 범위 IQR = 제 3사분위수 - 제 1사분위수 = Q3-Q1
- 범위
- 전체 관측값이 퍼진 정도
- 사분위수 범위
- 관측값의 중산 50%에 대한 범위
표준편차, 범위, 사분위수 범위의 비교
- 평균의 특징 = 표준편차의 특징
- 중앙값의 특징 = 사분위수 범위의 특징
- 표준편차
- 전체 관측값의 퍼진 정도를 골고루 반영
- 단점: 극단적인 관측값에 의해 영향을 받음
- 사분위수 범위
- 극단값의 영향없이 퍼진 정도를 확인 가능
- 단점: 제1사분위수와 제3사분위수 사이의 관측값에 대한 분포를 반영하지 않음
- 범위
- 퍼진 정도를 나타냄
- 단점: 표준편차의 단점과 사분위수 범위의 단점을 모두 가지고 있음
변동계수
- 퍼진 정도를 상대적으로 나타내는 수치를 사용
- 변동계수는 평균에 대한 상대적인 퍼진 정도를 백분율(%)로 나타냄
변동계수 CV = 표준편차/평균*100
- 비교 대상의 단위가 다른 겨우, 단위가 없는 변동계수를 통해 퍼진 정도 비교 가능
도수분포표와 상자그림
도수 분포표
- 자료가 도수분포표로 요약되고 원 자료는 주어지지 않을 경우
- 계급구간의 모든 관측값이 계급의 중간값을 갖는다고 가정하여 평균과 분산을 계산
- 원 자료를 그룹화에 의해 정보가 상실되기 때문에 가능하다면 원 자료를 이용
도구분포표에서의 평균
도구분포표에서의 분산, 표준편차
상자 그림
plt.boxplot()
- 다섯 가지 요약 수치(최솟값, Q1, Q2, Q3, 최댓값)를 그림으로 표현
- 일반적 그래프에선 드라나지 않는 수치를 함께 제공
- 제 1사분위수에서 제 3사분위수까지 상자로 그림
- 좌우에 선을 그러 최솟값, 최댓값을 나타냄
- 상자-수염그림(box-whisker plot)이라고도 함
- 봉우리가 하나 있는 분포의 특징을 나타내는데 적절
- 봉우리가 여러개 있는 분포에서는 효과적인 분석 어려움
- 대략적인 자료의 분포를 먼저 파악 후 상자 그림 작성
두 변수 자료의 요약
- 일반적 자료 요약
- 하나의 변수에 대한 관측 자료
- 도표/수치로 요약
- 두 변수 자료의 요약
- 둘 또는 그 이상 변수에 대한 관측 자료
- 동시에 분석하여 도표/수치로 요약
- 자료
- 범주형 자료(분할표)
- 수치형자료(산점도, 공분산, 상관계수)
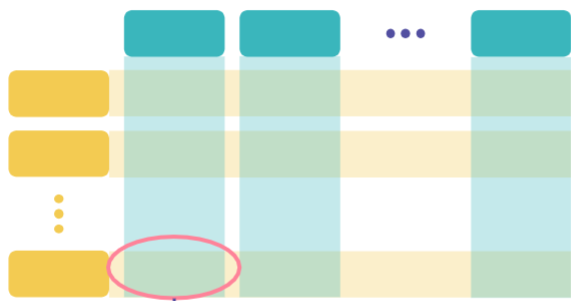
분할표
pd.crosstab(변수1, 변수2)
- 범주형 변수 2개 사용
- 도수분포표를 2차원으로 확장한 형태로 요약
- 교차하는 부분에 여러 가지 값 표시 가능
- ex) 상대도수 -> 두 변수 사이 관련 분포 상태를 명확히 표현
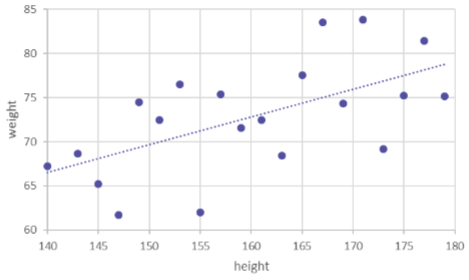
산점도(Scatter Plot)
plt.scatter(변수1, 변수2)
- 각 변수의 관측값을 좌표평면에 표시함
- 두 변수 사이의 관계를 시각적으로 파악
- 관측값이 많은 경우 점들이 띠를 형성
- 두 변수가 서로 어떤 관계인지 확인하기 위해 산점도를 사용
공분산
변수가 포함된 자료.cov()
- 두 변수(x, y)에 대하여 서로 어떤 관계를 가지는지 나타냄
- x값과 y값이 같은 방향으로 변화할 때, 공분산 값은 양수
- x값과 y값이 반대 방향으로 변화할 때, 공분산 값은 음수
- Cov(x,y)로 표현
- 두 변수의 편차를 곱하여 더한 후 자료의 개수(N)으로 나누어줌
- 자료가 평균값으로부터 얼마나 멀리 떨어져 있는지 나타냄
## 상관계수
변수가 포함된 자료.corr()
- 산점도의 점들이 직선에 가까운 정도를 수치로 나타내어 관계를 파악
- 두 변수(x, y)에 대하여 관측값 n개의 짝
- 표본상관계수 r은 항상 -1과 1사이에 있음
- 절댓값의 크기는 직선관계에 가까운 정도를 나타냄
- 부호는 직선관계의 방향을 나타냄
- r>0
- 점들이 좌하에서 우상방향으로 띠를 형성
- 두 변수의 값이 비례 관계를 나타냄
- 이 경향 직선의 기울기는 양수
- r<0
- 점들이 좌상에서 우하방향으로 띠를 형성
- 두 변수의 값이 반비례 관계를 나타냄
- 이 경향 직선의 기울기는 음수
- r+=1
- 모든 점이 정확히 기울기가 양수인 직선에 위치
- r-=1
- 모든 점이 정확히 기울기가 음수인 직선에 위치
- 상관계수의 특징
- 상관계수의 단위가 없음
- 변수 x,y의 단위는 분모, 분자에서 상쇄
- 이를 이용하여 단위가 다른 변수에서 직선관계 정도를 비교가능
- 상관계수만으로 판단 시, 잘못된 해석 가능성
- 상관계수는 직선 관계 나타내므로 직선이 아닐 때 부적합
- 상관계수를 구하기 전 산점도를 보고 전체의 경향을 파악한 후 상관계수 계산
- 상관계수의 단위가 없음
- 상관계수와 인과관계
- 인과관계
- x가 y의 원인이 되고 있다고 믿어지는 관계
- 자료 분석 시, 주의해야할 점
- 큰 상관계수값이 항상 두 변수 사이의 어떠한 인과관계를 의미하지 않는다는 사실 ``` 상어에 물린 사고 횟수가 늘어날 때 아이스크림 판매량도 같이 늘어난다
- 인과관계
-> 상어에 물린 사고 횟수와 아이스크림 판매량은 상관 관계가 있다 -> 상어에 많이 물릴 수록 아이스크림이 많이 팔린다
상어 사고가 많다 -> 해수욕이 많은 여름철이기 때문 아이스크림이 많이 팔린다 -> 더운 여름철이기 때문
직접적인 인과관계는 상어와 아이스크림이 아니라, 여름과 상어, 여름과 아이스크림에 있다 ```
- 상관 계수가 높다 != 인과관계이다




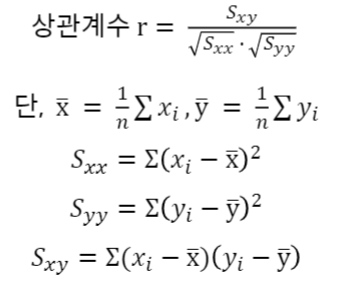
Leave a comment