1장. 시각화를 통한 자료의 요약
Updated:
자료의 형태
수치형 자료
- 양적 자료(Quantitative data)
- 수치로 측정이 가능한 자료
- 예) 키, 몸무게, 시험점구, 나이
- 선형 회귀 분석 등 사용
연속형 자료
- 연속적인 관측점을 가짐
- 원주율(3.1415623878…)
- 시간(09:12:23.21…) 등
이산형 자료
- 셀 수 있는 관측값을 가짐
- 예) 동영상 조회수
수치형 자료 구분
- 연속형 자료 != 이산형 자료
- 연속형 자료는 연속적인 관측
예) 시간 측정
어떤 순간은 09:12:23.21... 처럼 연속되고
있는 상태를 관측한 연속형 자료이나
평소에는 09시 12분으로 반올림하여
표현하여 이산령 자료로 사용
범주형 자료
- 질적자료(Qualitative data)
- 수치로 측정이 불가능한 자료
- 예) 성별, 지역, 혈액형 등
- 로지스틱 회귀 분석 등 사용
순위형 자료(Ordinal data)
- 범주 사이의 순서에 의미가 있음
- 예) 학점(A+, A, A-)
명목형 자료(Norminal data)
- 범주 사이에 순서에 의미가 없음
- 예) 혈액형(A, B, O, AB)
자료의 형태 구분시, 주의점
- 범주형 자료와 수치형 자료의 구분 != 자료의 숫자 표현 가능 여부
- 범주형 자료가 숫자로 표현되는 경우
남녀 성별 구분 시, 남자를 1, 여자를 0으로
표현하는 경우, 숫자로 표현되었으나
범주형 자료
- 수치형 자료를 범주형 자료로 변환하는 경우
나이 구분 시, 나잇값은 수치형 자료지만
10~19, 20~29세 등 나이대에 따라 구간화하면
범주형 자료
범주형 자료 요약
- 다수의 범주가 반복해서 관측
- 관측값의 크기보다 포함되는 범주에 관심
- 각 범주에 속하는 관측값의 개수를 측정
- 전체에서 차지하는 각 범주의 비율 파악
- 효율적으로 범주 간의 차이점 비교 가능
도수 분포표
- 도수(Frequency)
각 범주에 속하는 관측값의 개수
value_counts()
- 상대도수(Relative Frequency)
도수를 자료의 전체 개수로 나눈 비율
value_counts(normalize=True)
- 도구분포포(Frequency Tablej)
범주형 자료에서 범주와 그 범주에 대응하는 도수,
상대도수를 나열해 표로 만든 것
도수분포표를 구하는 파이썬 코드
# 한 가지 범주의 도수 분포표
pd.crosstab(index = 범주, columns = 'count')
# index로 설정한 범주에 해당하는 도수를 계산하여 도수분포표 제작
# 두 가지 범주의 도수 분포표
pd.crosstab(index = 범주, columns = 또 다른 범주)
# index로 설정한 범주와 columns로 설정한 범주를 모두 만족하는
# 도수를 계산하여 도수분포표 제작
- 몇 개의 범주를 기준으로 둘 것인지에 따라 다양한 도수분포표를 만들 수 있습니다
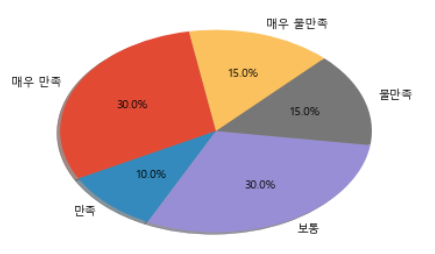
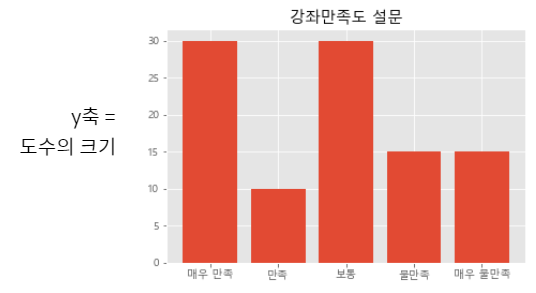
도수분포표 예시
- 강의 만족도 설문(100명 조사)
| 제목 | 내용 | 설명 | 설명 |
|---|---|---|---|
| 매우 만족 | 30 | 0.3 | 0.3 |
| 만족 | 10 | 0.1 | 0.4 |
| 보통 | 30 | 0.3 | 0.7 |
| 불만족 | 15 | 0.15 | 0.85 |
| 매우 불만족 | 15 | 0.15 | 1.00 |
원형그래프(Pie Chart)
plt.pie(수치, labels = 라벨)
- 숫자의 나열보다 전체적인 분포를 이해하기 쉬운 그래프
원을 각 범주가 차지하는 비율로 중심 각을 나누어
피자처럼 조각을 나눈 형태의 그림
- 장점
- 전체에서 범주가 차지하는 비율을 파악하기 쉬움
- 단점
- 범주 간 도수 비교 및 도수 크기 차이 파악이 어려움
막대그래프(Bar Chart)
plt.bar(수치, labels = 라벨)
- 각 범주에서 도수의 크기를 막대로 그림
그래프의 y축: 도수에 대한 눈금
그래프의 x축: 범주를 나열
- 장점
- 각 범주가 가지는 도수의 크기 차이를 비교하기 쉬움
- 단점
- 각 범주가 차지하는 비율의 비교는 어려움
수치형 자료의 요약
이산형 자료 요약
- 관측된 수치 자료가 셀 수 있는 경우 -> 이산형 자료 요약
- 관측값의 종류 수
- 많음 -> 범주형 자료 요약 기법
- 적음 -> 연속형 자료 요약 기법
연속형 자료 요약
- 수치 자료가 연속적으로 관측 -> 연속형 자료 요약
- 관측값의 종류 수
- 많음 -> 연속형 자료 요약 기법
- 적음 -> 점도표, 도수분포표, 히스토그램, 상대도수다각형, 줄기-잎 그림
점도표
- 관측값의 개수가 상대적으로 적은 경우(20 또는 25이하) 사용
- 자료 전체의 개요를 파악 가능
- 모든 자료를 나타낼 수 있도록 줄 위에 각 관측값에 해당되는 점을 찍어 표시
- 연속형 자료의 경우 중복된 정보를 판단하기 어려움 -> 자료를 크기에 따라 묶어서 분석하는 것이 효율적
도수 분포표
- 각 관측값에 대한 도수를 측정하여 도수분포표 작성
- 연속형 자료의 경우 다수의 구간(계급)으로 나누고 각 구간 마다 관측값의 개수(도수)로 작성
- 계급: 나눈 구간
- 계급구간: 각 계급에 포함되는 값의 범위
- 계급구간의 폭: 계급구간의 크기
도수분포표 작성 순서
- 자료의 범위: 자료에서 최대값 최소값을 찾아 자료의 범위를 구함
- 계급의 폭: 계급의 개수를 분포의 경향이 잘 드러날 수 있도록 정함
- 계급구간: 모든 관측 값을 포함하도록 계급구간의 경계점을 구함
- 도수: 각 계급구간에 속하는 관측값의 개수를 세어 계급의 도수를 더함
- 상대도수: 각 계급의 도수를 전체 관측값의 개수로 나눠 계급의 상대도수를 구함
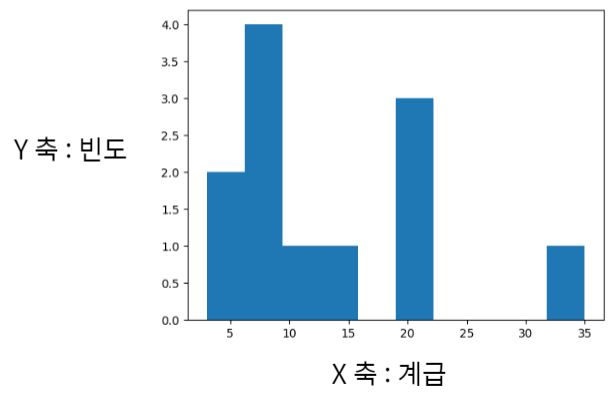
히스토그램
plt.hist()
- 연속형 자료의 도수분포표를 기반으로 각 계급을 범주처럼 사용 범주형 자료의 막대그래프와 같은 방식으로 그림
- 도수 비교 -> 범주: 막대그래프, 연속: 히스토그램
히스토그램의 특징
- 자료의 분포를 알 수 있음
- 계급구간과 막대의 높이로 그림
- 모든 계급구간의 폭이 같으면 도수, 상대도수를 막대 높이로 사용
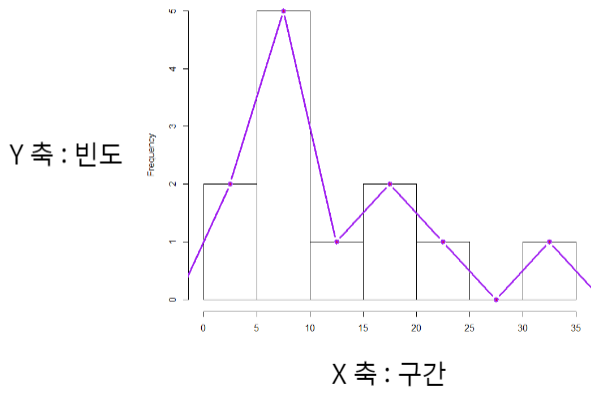
도수다각형
도수다각형의 특징
- 각 계급구간의 중앙에 점을 찍어 직선으로 연결함
- 관측값의 집중된 위치, 정도, 치우친 정도, 꼬리의 두터움등 분포의 상태를 쉽게 파악
- 관측값의 변화에 따라 도수 또는 상대도수의 변화를 잘 나타냄
도수다각형의 히스토그램
- 히스토그램: 옆으로 나열하여 자료 비교
- 도수다각형: 꺾은선으로 표시하여 자료 비교
- 여러 자료를 비교하기 위해서는 히스토그램보다 도수다각형이 알맞음
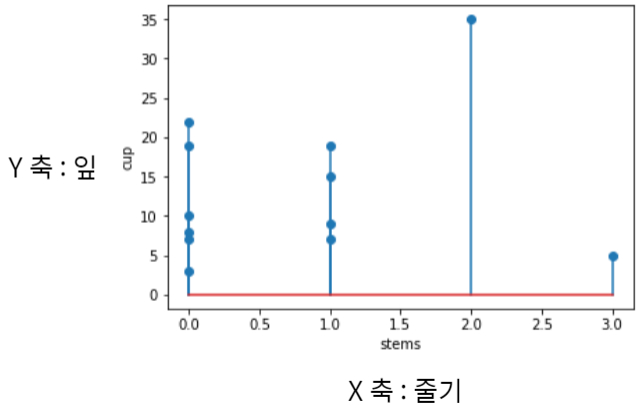
줄기-잎 그림
줄기-잎 그림 자료 정리 방법
- 예) 관측값의 자릿수가 최대 2자리 일때 -> 관측값 35 = 앞단위 3 + 뒷 단위 5
- 관측값을 보고 앞 단위와 뒷 단위를 정함
- 앞 단위를 줄기로 하여 세로로 배열하고 수직선을 그림
- 뒷 단위를 잎으로 하여 관측값을 앞 단위 오른쪽에 오름차순 기입
줄기-잎 그림자료 정리 예시
줄기-잎 그림 함수
plt.stem(줄기, 관측 값)
- 자료의 분포를 시각적으로 쉽게 파악
- 각 관측값도 유지 가능
- 함수 사용시에 줄기 값을 따로 지정해줘야 함: 줄기를 데이터마다 다르게 설정할 수 있기 때문
줄기-잎 그림 장단점
- 장점
- 관측값을 보여주므로 최대값, 최솟값등의 위치 파악 쉬움
- 순서대로 배열된 관측값의 장점과 히스토그램의 장점을 모두 가지고 있음
- 그리기 쉬움
- 단점
- 관측값의 개수가 많은 경우 제한된 공간에 그리기 불가능
- 관측값이 지나치게 흩어져 있으면 부적절


Leave a comment