머신러닝을 위한 수학_2
Updated:
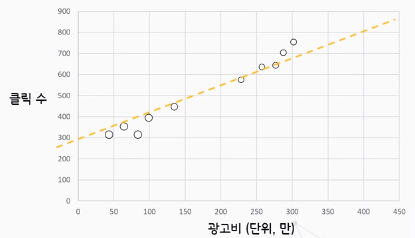
머신러닝을 적용시키는 방법은 쉽게는 함수을 만드는 것이다.
- 위의 그래프에서는 기울기와 절편을 찾는것이 목표이다
-
Noidy Data
항상 모든점을 정확히 지나지는 않는다. - 머신러닝의 핵심
- 과거의 관측을 기반으로 새로운 샘플의 결과값을 예측
- 우리가 바라는 이상
- 적합한 가중치와 절편 탐색 => 실제 결과값과 예측 결과값의 차이를 찾아 0을 만드는 것
- 우리의 목표
- 모든 점에서 생기는 오차의 합계가 가능한 작아지는 함수를 찾는것
- 적용되는 식을 만드는 것 => 목적함수
1. 목적함수
- 각각의 학습 데이터마다, 실제 결과값과 예측한 결과값의 오차를
제곱해서 그것을 모두 더하고, 또 그것에 1/2을 곱해준다.
- 오차값들의 상쇄를 방지하기 위해 제곱
-
1/2은 미분과 관련이 있다. 결과식을 간단한 모양으로 만들기 위한 상수
최소값의 위치는 변함이 없다
1 .최적화 문제
- 위의 목적 함숫값이 가장 작아지는 파라미터들을 찾는 것
2. 경사 하강법
- 최적화 문제
- 적절한 파라미터를 찾기위해 가중치와 절편을 탐색하는 기법
- 목적함수의 값을 최소화 시키기 위해 마치 경사를 내려가는 듯 최소값을 찾는 기법
1. 미분
- 간격을 좁혀서 순간 기울기를 구하는것
-
-
도함수
미분후 나온 함수 - 도함수의 부호 반대 방향으로 밀면 자연스럽게 최소값 쪽으로 움직인다.
경사하강법
A:=B A를 B에 따라 정의한다.
2. 학습률(η)
- 양의 정수 사용
- 학습률에 따라 최소값에 도달하기까지 갱신(수렴)하는 속도가 달라진다.
- 값이 작을수록 정확하지만 시간이 오래걸린다.
η = 1 발산 현상 관측
η = 0.1 수렴 속도 지연
3. 편미분
미분할 변수에만 주목하고 다른 변수는 상수 취급
- 머신러닝의 최적화 문제는 매개변수의 개수만큼 변수가 있으므로
목적함수가 다변수 함수의 형태로 등장한다 - 상수 미분시 0
1. 합성함수
- 복잡한 함수는 단순한 함수로 구성된 합성함수로 생각하고 미분을 진행한다
- 여러 함수의 조합
- 갱신식을 위한 목적함수의 매개변수 편미분 과정
- θ제로로 미분 과정
결과
- θ제로로 미분 과정
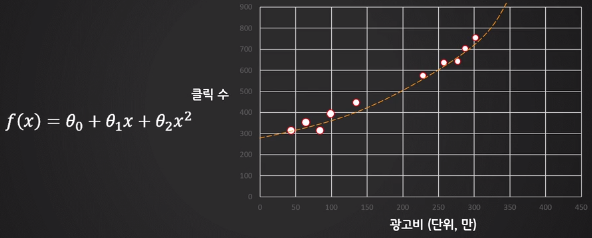
- 2차함수가 더 정확할지도 모른다
- 차수를 크게하면 정확할지 모르지만 과적합이 발생된다.
2. 다항식 회귀
- 다항식의 차수를 늘린 함수를 사용하는 것
- 일반화

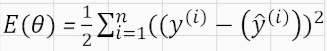
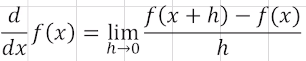
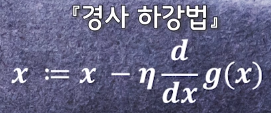


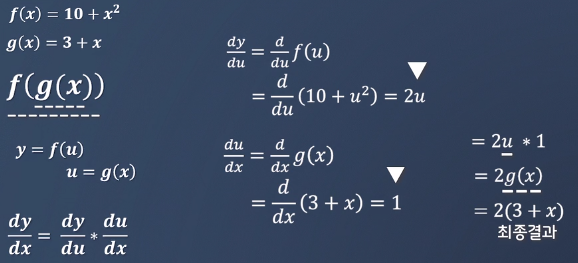


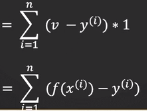
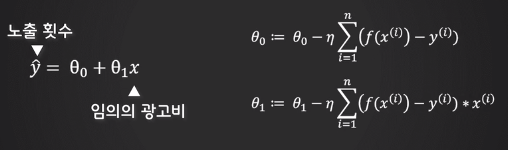

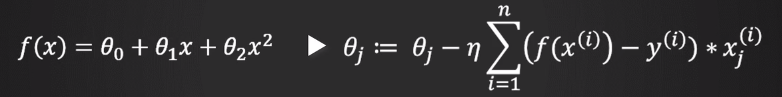
Leave a comment