머신러닝을 위한 수학_1

머신 러닝 기반의 확률과 통계

1. 통계학의 용어와 통계 모델링

1. 통계학

• 수치 데이터의 수집, 분석, 해석, 표현 등을 다루는 수학의 한 분야

1. 기술 통계학

• 연속형 데이터
  • 키/나이/가격 => 평균/표준편차
• 범주형 데이터
  • 이름/종족/성별 => 빈도/백분율

2. 추론 통계학

• 표본의 통계분석을 바탕으로 전체에 대한 결론을 유추
• 가설검정

2. 통계 모델링

• 데이터에 통계학을 적용하여 변수의 유의성을 분석함으로써 방대한 양의 데이터에 숨겨진 특징을 찾아내는 것을 의미

• 통계모델(수학적모델)

  수학식을 계산하여 실제 값을 추정하는 방법
  

• 여러가정을 가지고 있고, 이 가정들은 확률 분포를 따른다

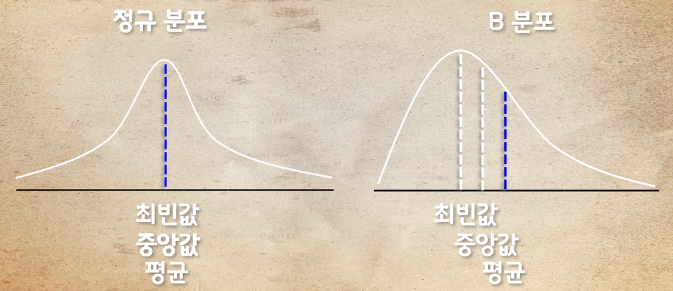
1. 확률 분포

• 최빈값

  분포상 가장 많은 빈도수를 가진 값
  가장 높은 위치의 값
  

• 중앙값

  값들을 정렬 했을 때 순서상 중앙에 위치하는 값
  정규 분포에서는 최빈값과 같은 중앙에 위치
  

• 평균

  모든 데이터들의 평균값
  정규 분포에서는 최빈값과 중앙값과 같은 중앙에 위치
  

2. 이론

1. 변량의 측정

• 수치, 변수
• 산포(데이터의 변량) : 데이터가 얼마나 중심으로 모이지 않고 흩어저 있는지

2. 분산

• 평균과의 거리를 제곱한 값의 평균

3. 표준편차

• 분산의 제곱근
• 분산은 값이 너무 커서 비교하기가 쉽지 않아 표준편차를 사용

4. 사분위수

• 데이터 구성을 전체적으로 살펴보고자 할 때 사용
• 데이터의 이상치 탐색과 중심위치 및 분포를 빠르게 파악할 수 있다는 강점
  1. 데이터들을 크기순으로 가장 작은 값부터 가장 큰값까지 정렬
  2. 25% 1사분위수, 50% 2사분위수, 75% 3사분위수, 100% 4사분위수,
  3. 범위가 짝수인 경우 각 단면의 값들의 ‘평균’을 구해 표현
     
     
     b사의 600을 제거한다.
• IQR(InterQuartile Range)
  • 이상치 탐색, 데이터의 분포 등을 확인할 때 유용
  • 다수의 객체들과 비교하고자 할때 유용 사분범위의 1.5배를 기준으로 산정