머신러닝 - 분류 문제
Updated:
-
머신러닝 알고리즘의 선택 기준
1. 변수의 특성 2. 데이터의 개수 3. 노이즈 데이터의 양 4. 클래스의 선형적 구분 여부 -
머신러닝 알고리즘 훈련을 위한 단계
1. 변수를 선택하고 훈련데이터를 수집 2. 모델의 성능 지표를 선택 3. 분류 모델과 최적화 알고리즘을 선택 4. 모뎅의 성능 평가 5. 모델 튜닝
1. 퍼셉트론
- 여러개의 입력을 받아 각각의 값에 가중치를 곱한 후, 모두 더한 것이 출력되는 형태의 모델
- 단순모델
- 선형적이다. 선형적으로 구분되지 않는 데이터에는 수렴하지 못한다는 단점
2. 로지스틱 회귀
'분류를 확률로 생각하는 방식'
- 퍼셉트론의 간단함을 유지하면서 비선형적 문제 해결 가능
- 어느 클래스에 분류 되는지 구하는 것 => 함수 필요
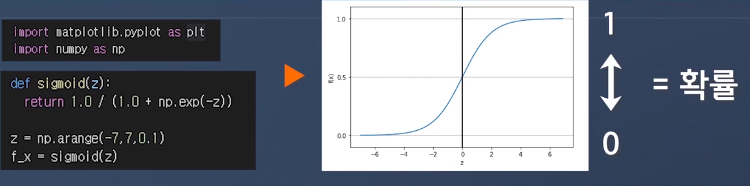
1. 로지스틱시그모이드함수
- 어떠한 입력값이 들어와도 0 ~ 1 사이의 값을 반환 이를 확률처럼 다룰수 있음
-
P(y = 1 x) = f(x) x값이 주어졌을때 y가 1일 확률 ex) f(x) = 0.7는 가로로 길확률이 0.7 -
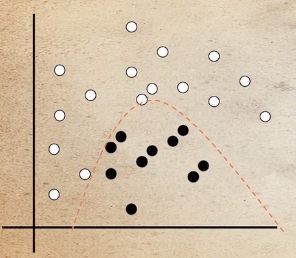
결정경계
두개로 구분할 때 사용하는 경계선
- 목적함구 정의
- 미분
- 매개변수 갱신식 구하기
- 곡선의 형태는 차수를 늘려준다
3. 서포트 벡터 머신(SVM)
- 강력한 학습 알고리즘
- 마진을 최대화
- 초평면(결정경계)
- 마진은 초평면과 가장 가까운 훈련 데이터(서포트 벡터)들 사이의 거리
- 일반화를 진행했을때 오차가 낮아지는 경향을 보임
-
선형분리 불가능 문제에서도 강력함을 보인다
2차원 => 3차원 비선형 결정경계에서도 사용가능함 분리 가능 공간을 생성한다 - 단점
- 계산비용 => 컴퓨팅 비용이 높다
- 커널 기법으로 어느정도 해결 가능
4. 결정 트리 학습
ex)범주형 변수
- 설명이 중요할때 유용
- 범주형 변수, 실수형 변수에 적용된다
- 리프(leaf)노드가 순수해질때까지 자식노드에서 분할 작업을 반복
- 깊은 트리가 만들어지면 과적합이 생김 => 트리의 최대깊이를 제한(가지치기-pruning)
-
목적함수의 목적
가장 정보가 풍부한 특성으로 노드를 나누기 위함 트리 알고리즘으로 최적화 - 각 분할에서 정보이득(IG) 최대화
- 자식 노드의 불순도가 낮을수록 정보이득(IG)는 커진다
ex)구현을 간단하게 하기위한 이진트리형태
- 엔트로피
- 한 노드의 모든 데이터가 같은 클래스라면 엔트로피는 0
- 반대로 클래스 분포가 균등하다면 엔트로피는 최대 1
- 트리의 상호 의존 정보를 최대화 하는 것
- 지니 불순도
- 엔트로피와 반대되는 개념
- 잘못 분류될 확률을 최소화 하기 위한 기준
- 분류오차
- 두 클래스가 같은 비율일때 최대값 0.5
- 노드의 클래스 확률 변화에 둔감 => 잘 사용안한다
5. K-최근접 이웃(KNN)
- 훈련과정을 진행하지 않은 머신러닝 알고리즘
- 알고리즘을 실행할 때마다 모든 학습데이터를 통해 분류를 진행
- 매번 실행할 때 마다 학습 데이터 필요하다는 단점
- 데이터 정제만 잘한다면 학습과정이 없으니
빠르게 결과를 살펴볼수 있는 장점이 있다.
- 숫자 K와 거리 측정 기준을 선택(유클리디안 거리 측정 방식)
- 분류하려는 미지의 데이터에서 K개의 최근접 이웃을 찾습니다(우리가 설정한 K값)
- 다수격 투표를 진행, 투표 결과에 따라 미지의 데이터 클래스 레이블을 할당
- 과적합과 과소적합 사이에서 올바른 K값을 찾는 것이 매우 중요
-
차원의 저주
고정된 크기의 훈련 데이터셋 차원이 늘어남에 따라 특성 공간이 점점 희소해지는 현상- 올바른 변수 선택
- 차원 축소 기법

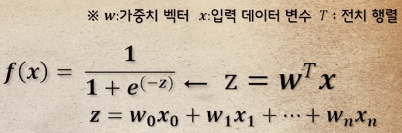



Leave a comment