실습_4. 선형대수_벡터와 행렬

실습

벡터

파이썬에서 벡터와 행렬을 표현하기 위한 라이브러리에는 numpy가 있습니다. 사실 상 표준이라고 불릴 정도로 많은 수학이나 머신러닝 관련 라이브러리에서 numpy를 기본 자료형으로 사용합니다.

numpy에서는 벡터와 행렬 모두 numpy 배열이라는 동일한 자료형으로 다루어 집니다. 둘을 구분하는 것은 배열의 차원을 기준으로 합니다. 벡터도 1xn, nx1의 행렬로 간주합니다.

다음은 1차원 리스트를 numpy 행벡터로 변환하여 벡터합을 계산하는 예제입니다. np.array함수로 numpy 배열을 생성할 수 있습니다.

>>> import numpy as np
>>> a = np.array([[1, 2, 3]])
>>> print(type(a))
<class 'numpy.ndarray'>
>>> b = np.array([[4, 5, 6]])
>>> print(a+b)
[[5 7 9]]

스칼라 곱은 단순히 수를 곱하면 됩니다.

>>> print(2*a)
[[2 4 6]]

길이가 같은 두 리스트가 주어졌을 때 다음과 같은 연산을 하는 함수를 작성해 봅시다.

numpy 행벡터로 변환 식 5(a+b) 계산

• 입력

a: 리스트  
b: a 와 길이가 같은리스트

• 출력

문제에서 주어진 식의 결과 행벡터 numpy 배열

• 실행 결과

>>> vec_calc([1, 2, 3], [4, 5, 6])
array([[25 35 45]])
>>> vec_calc([26], [80])
array([[530]])
>>> vec_calc([65, 95, 18, 78], [9, 19, 9, 70])
array([[370 570 135 740]])

• 이렇게 해보세요!

입력으로 받은 두 리스트를 각각 1xn, 즉 [[1,2,3]] 꼴로 만든 뒤 np.array함수를 사용해 numpy 배열로 변환해보세요.

변환된 numpy 배열에 더하기, 스칼라곱 연산을 시도해보세요.

import numpy as np

def vec_calc(a, b):
    a = np.array([a])
    b = np.array([b])
    
    return 5*(a+b)
    
print(vec_calc([1, 2, 3], [4, 5, 6]))

행렬

행렬을 numpy 배열로 변환하는 방법도 벡터와 동일합니다.

>>> A = np.array([[1,2], [3, 4], [5, 6]])
>>> print(A)
[[1 2]
 [3 4]
 [5 6]]

행렬곱은 np.matmul 함수를 사용하면 됩니다.

>>> A
array([[1, 2, 3],
       [4, 5, 6]])
>>> B
array([[1, 2],
       [3, 4],
       [5, 6]])
>>> np.matmul(A, B)
array([[22, 28],
       [49, 64]])

두 numpy 배열 A, B가 주어졌을때 다음의 계산을 하는 함수를 작성해 봅시다.

5(A×B)

• 입력

A: numpy 행렬  
B: A와 행렬곱이 가능한 numpy 행렬

• 출력

문제에서 주어진 식의 결과

• 실행 결과

>>> mat_calc(
...     np.array([[1, 2, 3], [4, 5, 6]]),
...     np.array([[1, 2], [3, 4], [5, 6]])
... )
array([[110 140]
                            [245 320]])

• 이렇게 해보세요!

이미 입력이 numpy 배열이므로 변환 없이 바로 행렬곱, 스칼라곱 연산자를 시도해보세요.

import numpy as np

def mat_calc(A, B):
    
    return 5*np.matmul(A, B)
    
print(mat_calc(np.array([[1, 2, 3], [4, 5, 6]]), np.array([[1, 2], [3, 4], [5, 6]])))

대각행렬

numpy에서는 다양한 행렬을 쉽게 생성할 수 있도록 많은 함수를 제공하고 있습니다. 예를 들어 0으로만 채워진 행렬을 만들고 싶다면 np.zeros 함수를 사용해 볼 수 있습니다.

다음 예제는 0으로 채워진 3x4 행렬을 만드는 예제입니다.

>>> np.zeros((3, 4))
array([[0., 0., 0., 0.],
       [0., 0., 0., 0.],
       [0., 0., 0., 0.]])

0이 아니고 0. 으로 표기되는 이유는 기본 자료형이 정수형이 아닌 부동소수점으로 설정되기 때문입니다.

어떤 수 n이 주여졌을 때 1, 2, 3, …, n을 대각성분으로 가지는 대각행렬을 만드는 함수를 작성해 봅시다.

• 입력

n: 대각행렬의 성분 수

• 출력

1, 2, 3, ..., n을 대각성분으로 가지는 대각행렬

• 실행 결과

>>> n_diag(1)
array([[1]])
>>> n_diag(2)
array([[1 0]
       [0 2]])
>>> n_diag(3)
array([[1 0 0]
       [0 2 0]
       [0 0 3]])

• 이렇게 해보세요!

np.diag 함수를 사용해서 대각행렬을 쉽게 만들어보세요. 레퍼런스

np.diag 함수의 인자로는 range를 이용해보세요.

import numpy as np

def n_diag(n):
    arr = [i for i in range(1,n+1)]
    return np.diag(arr)
    
print(n_diag(3))

역행렬

앞서 이론에서 2x2 행렬의 역행렬을 직접 계산하는 방법을 알아보았습니다.

역행렬을 계산하기 위해서 np.linalg.inv 함수를 사용할 수도 있지만 여기서는 2x2 행렬의 역행렬을 계산하는 함수를 직접 구현해 봅시다.

• 입력

A: 2x2 크기의 numpy 행렬

• 출력

A의 역행렬. 만약 역행렬이 존재하지 않다면 None을 리턴.

• 실행 결과

>>> mat_inv(np.array([[1, 2], [3, -1]]))
array([[ 0.14285714,  0.28571429],
       [ 0.42857143, -0.14285714]])
>>> mat_inv(np.array([[1 1], [1 1]]))
None

• 이렇게 해보세요!

입력으로 받은 행렬의 각 원소를 a, b, c, d로 저장해보세요.

역행렬을 만드는 공식에 따라 a, b, c, d를 사용해 역행렬을 계산해보세요.

행렬식 ad-bc가 0이라면 None을 리턴하도록 해보세요.

import numpy as np

def mat_inv(A):
    # 1. 가역행렬인지 확인해보세요.
    a, b, c, d = A[0][0], A[0][1], A[1][0], A[1][1]
    det = a*d-b*c
    if det == 0:
        return
    # 2. 가역행렬이라면 역행렬을 반환해주세요
    return 1/det * np.array([[d, -b],[-c, a]])
    
print(mat_inv(np.array([[1, 2], [3, -1]])))

행렬과 연립방정식

행렬의 사용법 중 하나는 연립방정식의 해결입니다.

다음과 같은 식의 벡터해 x를 구하는 함수를 작성해 봅시다.

Ax=y

이번 실습에서는 역행렬을 만들기 위해 np.linalg.inv를 사용해보아도 좋습니다.

• 입력

A: 역행렬이 존재하는 numpy 행렬  
y: numpy 열벡터

• 출력

문제의 식을 만족하는 열벡터 x

• 실행 결과

>>> mat_solve(
... np.array([[1, 2], [3, -1]]),
... np.array([[1], [0]]))
array([[0.14285714],
      [0.42857143]])
>>> mat_solve(
... np.array([[4, 5], [6, 7]]),
... np.array([[82], [ 9]]))
array([[-264.5]
       [ 228. ]])

• 이렇게 해보세요!

np.linalg.inv함수를 사용해서 A의 역행렬을 구해보세요. 레퍼런스

A의 역행렬과 y를 행렬곱하여 x를 구해보세요.

import numpy as np

def mat_solve(A, y):
    # 역행렬을 만들어서 A의 역행렬과 y를 곱하여 반환해보세요.
    A_i = np.linalg.inv(A)
    return np.matmul (A_i, y)
    
print(mat_solve(np.array([[1, 2], [3, -1]]),np.array([[1], [0]])))

컨볼루션 연산

2D 컨볼루션 연산은 이미지 II에 커널 KK를 슬라이딩해가며 성분곱 후 원소의 합을 구하는 연산을 말합니다.

numpy를 사용해서 2D 컨볼루션 연산을 직접 구현해봅시다. 패딩은 없으며 스트라이드값은 1이라고 가정합니다.

※ 커널을 뒤집지 않고 계산합니다.

• 입력

I: 이미지
K: 커널

• 출력

I와 K의 2D 컨볼루션 결과

• 실행 결과

>>> conv2d(np.array([[0, 1, 1, 1],
...                  [0, 0, 1, 1],
...                  [0, 0, 0, 1],
...                  [1, 0, 0, 1]]),
...        np.array([[1, -1],
...                  [1, -1]]))
array([[-1, -1,  0],
       [ 0, -1, -1],
       [ 1,  0, -2]])
>>> conv2d(np.array([[ 0,  1, -1,  1],
...                  [ 1,  0,  1, -1],
...                  [ 0, -1,  0,  1],
...                  [ 0,  1,  0,  0]]),
...        np.array([[1, 1, 1]]))
array([[ 0.  1.]
       [ 2.  0.]
       [-1.  0.]
       [ 1.  1.]])

• 이렇게 해보세요!

np.zeros로 결과에 해당하는 크기를 가진 빈 행렬을 하나 만들어보세요.

II의 각 부분에 접근할 수 있도록 반복문을 작성해보세요.

II의 일부와 KK를 * 연산자로 합성곱 후 모두 더한 결과를 처음에 만든 행렬에 할당해보세요.

import numpy as np

def conv2d(I, K):
    # 1. 이미지와 커널의 합성곱을 한 후, 그 결과에 해당하는 크기를 가진 빈 행렬을 만들어보세요.
    ze = np.zeros((len(I)-len(K)+1,len(I[0])-len(K[0])+1))
    # 2. 컨볼루션 연산을 위한 반복문을 선언해보세요.
    for i in range(len(ze)):
        for j in range(len(ze[0])):
            a = I[i:i+len(K),j:j+len(K[0])]*K
    # 3. I의 부분행렬(Kh * Kw)과 K의 합성곱을 한 후, 모두 더한 값을 새로운 행렬로 만들어보세요.
            ze[i][j] = a.sum()
    # 4. 결과를 반환해보세요.
    return ze
    
print(conv2d(np.array([[0, 1, 1, 1], [0, 0, 1, 1], [0, 0, 0, 1], [1, 0, 0, 1]]), np.array([[1, -1], [1, -1]])))

미션

벡터의 내적

벡터의 내적은 두 벡터의 원소별 곱의 합을 구하는 연산입니다.

두 리스트가 주어졌을 때 내적을 구하는 함수를 작성해 봅시다.

• 입력

a: 숫자 리스트  
b: a와 길이가 동일한 숫자 리스트

• 출력

벡터 a, b의 내적 값

• 실행 결과

>>> dot([1, 2, 3], [4, 5, 6])
array(32)
>>> dot([26], [80])
array(2080)
>>> dot([14, 28, 72, 74], [40, 23, 95, 5])
array(8414)

• 이렇게 해보세요!

주어진 리스트를 numpy 배열로 변환해보세요.

변환된 numpy 배열에 적절한 연산을 적용하여 내적의 값을 구해보세요.

계산된 벡터에서 값만 뽑아내어 결과 값으로 리턴하세요.

• Tip

내적을 구하기 위해 np.dot를 쓰거나 합성곱 (* 연산자) 후 np.sum을 쓰는 방법을 사용할 수 있습니다.

import numpy as np

def dot(a, b):
    # numpy의 dot은 두 배열의 내적곱을 구하는 함수로, 
    # np.dot(array1, array2)의 방식으로 사용할 수 있습니다.
    # 이를 활용하여 배열 a와 b의 내적곱을 구하고 이를 반환해보세요.
    return np.dot(a,b)
   
print(dot([1, 2, 3], [4, 5, 6]))

NumPy 인덱싱

numpy는 강력한 인덱싱 기능을 제공합니다. a[1:3,2:5]라고 실행하면 행렬 a의 1, 2행과 2, 3, 4열에 해당하는 2x3 크기의 부분 행렬을 얻을 수 있습니다. 여기에 할당 연산자 =로 2x3의 행렬을 대입하는 것도 가능합니다.

짝수 자연수 m, n이 주어졌을때 다음의 형태를 띠는 numpy 행렬을 만들어 봅시다. numpy의 인덱스 기능을 이용하면 더 쉽게 해결할 수 있습니다.

“중앙을 원점으로 각 사분면의 번호를 값으로 가지는 mxn 크기의 xy 평면 행렬”

# m, n = 2, 2
21
34

# m, n = 2, 4
2211
3344

# m, n = 6, 6
222111
222111
222111
333444
333444
333444

• 입력

m: 좌표 평면의 행 수
n: 조표 평면의 열 수

• 출력

문제의 조건을 만족하는 numpy 행렬

• 실행 결과

>>> mat_coord(2, 2)
array([[2, 1],
       [3, 4]])
>>> mat_coord(2, 4)
array([[2, 2, 1, 1],
       [2, 3, 4, 4]])
>>> mat_coord(6, 6)
array([[2, 2, 2, 1, 1, 1],
       [2, 2, 2, 1, 1, 1],
       [2, 2, 2, 1, 1, 1],
       [3, 3, 3, 4, 4, 4],
       [3, 3, 3, 4, 4, 4],
       [3, 3, 3, 4, 4, 4]])

• 이렇게 해보세요!

결과물의 크기에 해당하는 빈 행렬을 np.zeros로 만들어보세요.

numpy의 인덱싱을 기능을 사용하여 원하는 부분을 선택한 후 숫자를 대입해보세요.

• Tip

numpy 행렬에 스칼라 값을 대입하면 모든 원소에 그 값이 할당됩니다.

import numpy as np

def mat_coord(m, n):

    ze = np.zeros((m,n))
    
    ze[:m//2,:n//2] = 2
    ze[:m//2,n//2:] = 1
    ze[m//2:,:n//2] = 3
    ze[m//2:,n//2:] = 4
    
    return ze
    
# 결과 출력을 위한 코드입니다. 자유롭게 값을 바꿔보며 확인해보세요.
print(mat_coord(2, 4))

대칭행렬

대칭행렬은 행렬 A와 그 전치행렬인 A^T가 동일한 행렬을 말합니다.

주어진 행렬이 대칭행렬인지 확인하는 함수를 작성해 봅시다.

• 입력

A: 정사각행렬 numpy 배열

• 출력

A가 대칭행렬이면 True, 아니라면 False

• 실행 결과

>>> is_symmetric(np.array([[1, 2], [2, 3]]))
True
>>> is_symmetric(np.array([[1]]))
True
>>> is_symmetric(np.array([[1, 2], [3, 4]]))
False

• 이렇게 해보세요!

np.transpose로 주어진 행렬의 전치 행렬을 구해보세요. 레퍼런스

np.allclose를 사용하면 두 numpy 행렬의 모든 원소가 일치하는지 확인할 수 있습니다. 레퍼런스

• Tip

행렬을 비교할 때 == 연산자를 사용하면 원소별로 일치여부를 알려주는 True, Flase 행렬이 나옵니다. 두 행렬이 단순히 같은지를 확인하기 위해서는 np.allclose가 더 적합합니다.

import numpy as np

def is_symmetric(A):
    # A행렬의 전치를 구해서 B에 저장한다
    B = np.transpose(A)
    # 두 행렬이 같은지 확인해준다
    return np.allclose(A,B)
    
print(is_symmetric(np.array([[1, 2], [2, 3]])))

행렬변환

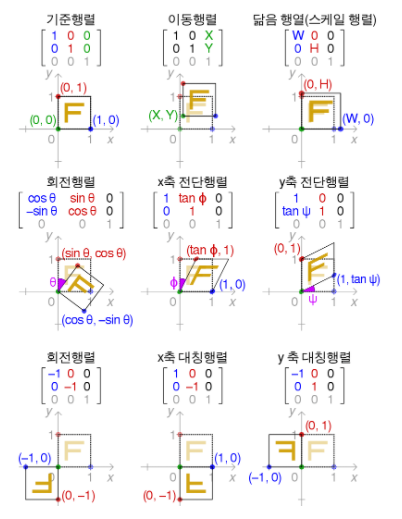
행렬은 마치 하나의 함수로써 사용될 수 있는데, 이를 이용한 계산을 행렬변환이라고 부릅니다. 2차 평면 위에 좌표 (x, y)에 해당하는 벡터 v=[x \ y \ 1]^Tv=[x y 1]는 특정한 행렬 A에 Av꼴로 곱해짐으로써 대칭, 확대, 축소, 회전 등의 변환이 가능합니다. v에 추가로 붙은 1은 이 벡터가 좌표벡터라는 의미이며 여기서는 변환행렬을 위한 조건 중 하나라고 이해하시고 넘어가면 되겠습니다. 변환의 결과 역시 [x \ y \ 1]^T[x y 1]꼴로 나타게됩니다.

※ 회전행렬은 좌표를 반시계방향으로 \thetaθ만큼 회전시키는 행렬변환입니다. 위 이미지의 회전 변환에서는 -\theta−θ만큼 회전변환하기에 시계방향으로 돌고 있습니다.

위 이미지를 참고하여 다음의 연산을 실행하는 함수를 작성해 봅시다.

1. y축 대칭
2. 시계 방향으로 90도 회전
3. x축으로 2배 확대

• 입력

v: [[x]  [y]  [1]]꼴의 열벡터 (numpy 배열)

• 출력

문제의 식을 적용한 [[x]  [y]  [1]] 꼴의 변환된 열벡터 (numpy 배열)

• 실행 결과

>>> transform(np.array([[1], [2], [1]]))
array([[4.], [1.], [1.]])
>>> transform(np.array([[-2], [ 5], [ 1]]))
array([[10.], [-2.], [ 1.]])
>>> transform(np.array([[0.5], [1. ], [1. ]]))
array([[2. ], [0.5], [1. ]])

• 이렇게 해보세요!

문제의 조건을 만족하기 위한 변환 행렬을 만들어보세요.

주어진 열벡터를 변환 행렬에 차례로 행렬곱하여 변환해보세요.

• Tip

행렬곱을 위해 np.matmul을 사용합니다.

행렬곱 시 변환행렬이 왼쪽, 변환될 벡터가 오른쪽에 있어야 의도한 계산이 됩니다.

import numpy as np
import math

PI = 3.14

def transform(v):
    # y 축 대칭 행렬
    y_Symmetry = np.array([[-1,0,0],[0,1,0],[0,0,1]])
    v = np.matmul(y_Symmetry, v)
    
    Cos_90 = math.cos(math.radians(90))
    Sin_90 = math.sin(math.radians(90))
    
    # 시계방향 90도 회전행렬
    rotate_90 = np.array([[Cos_90,Sin_90,0],[-Sin_90,Cos_90,0],[0,0,1]])
    v = np.matmul(rotate_90, v)
    
    # x 값 2배 행렬
    x_mul_2 = np.array([[2,0,0],[0,1,0],[0,0,1]])
    v = np.matmul(x_mul_2, v)
    
    return v
    
print(transform(np.array([[1], [2], [1]])))

컨볼루션 연산 2

컨볼루션 연산에서는 이미지 II의 크기와 커널 KK의 크기, 그리고 패딩 및 스트라이드의 값에 따라 결과의 크기가 달라지게 됩니다. 영향을 받는 원인이 많다보니 결과의 크기를 직관적으로 예측하기는 어려운 편입니다.

이미지 II의 크기, 커널 KK의 크기, 패딩 수, 스트라이드 값이 주어졌을때 I \circledast KI⊛K의 크기를 계산하는 함수를 작성해 봅시다.

• 입력

I: I의 크기 (h, w) 튜플  
K: K의 크기 (h, w) 튜플  
p: I의 패딩 수 (h, w) 튜플  
s: 컨볼루션의 스트라이드 값 (h, w) 튜플

• 출력

I와 K의 2D 컨볼루션 결과의 (높이, 너비)

• 실행 결과

>>> conv_size((5, 5), (3, 3), (0, 0), (1, 1))
(3, 3)
>>> conv_size((2, 2), (2, 2), (1, 1), (2, 2))
(2, 2)
>>> conv_size((6, 17), (1, 3), (1, 2), (1, 2))
(8, 10)

• 이렇게 해보세요!

높이와 폭의 계산을 따로 생각해보세요.

II에 패딩을 먼저 적용한 크기를 구한 뒤 KK를 스트라이드에 맞추어 몇번이나 II에 적용할 수 있는지 세어보세요.

• Tip

2D 컨볼루션의 K는 커널(Kernal)이며 필터(Filter)라고 부르는 F로 표기하기도 합니다.

참고

import numpy as np

def conv_size(I, K, p, s):
    I = np.array(I)
    K = np.array(K)
    p = np.array(p)
    s = np.array(s)
    
    return tuple((I - K + 2 * p)/s + 1)
    
print(conv_size((5, 5), (3, 3), (0, 0), (1, 1)))